Research progress and achievements of the National Natural Science Foundation of China

Adaptive FEM Analysis for Crak Damage Detection of Frame Structure (Grant No-51608301，Principal Investigator: Dr. Yongliang Wang)

Background  Research Contents  Research Achievements  Related links  Contact information

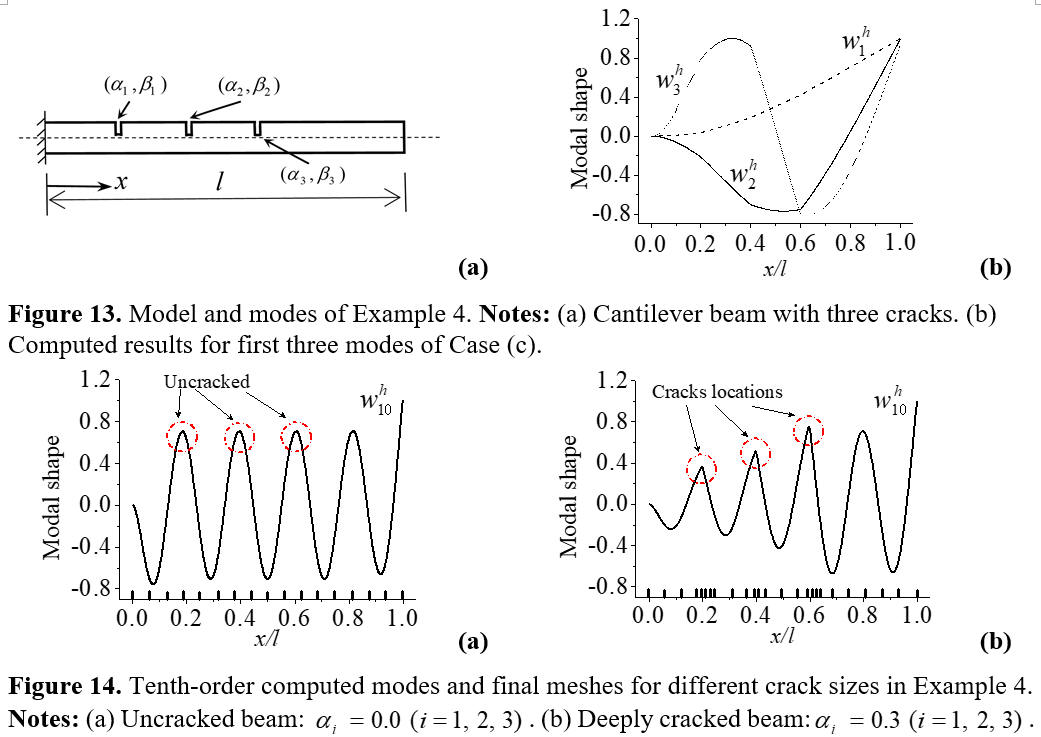
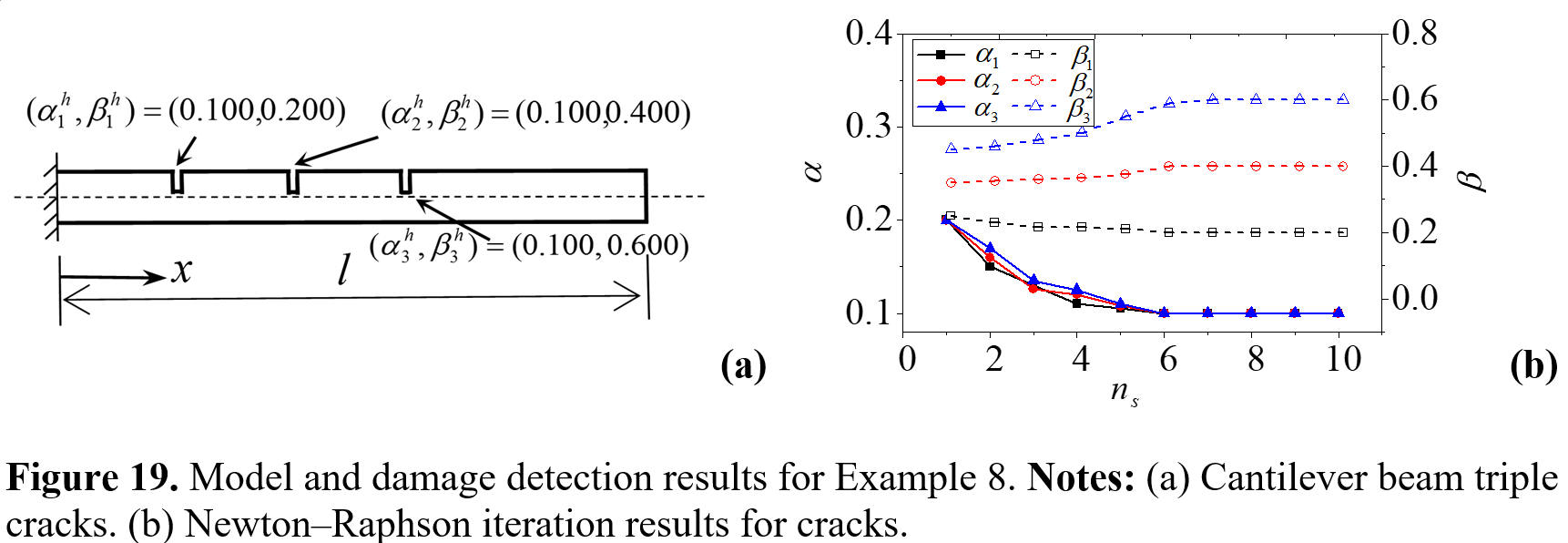
1. Yongliang Wang, Yang Ju, Zhuo Zhuang, Chenfeng Li. Adaptive finite element analysis for damage detection of non–uniform Euler–Bernoulli beams with multiple cracks based on natural frequencies. Engineering Computation. 2018. DOI: 10.1108/EC-05-2017-0176.

In this study, a new adaptive FEM methodology was presented for accurate computation of both the frequencies and modes of cracked Euler–Bernoulli beams, and the adaptive analysis technology has been developed and applicated for the reliable computation of the locations and sizes of multiple cracks. Some key techniques are utilized, i.e., adaptive FE analysis for eigensolutions, Newton–Raphson iteration, and damage refinement techniques, based on the conventional frequency measurement method for damage detection, which has yielded a simple and practical adaptive FE procedure that finds sufficiently fine meshes for the accurate locations and sizes of multiple cracks to match the pre-specified error tolerance. Numerical examples are provided, including ones known to be representative of a non-uniform and geometrically stepped Euler–Bernoulli beam with multiple cracks, to demonstrate the accuracy, reliability, and effectiveness of the proposed adaptive FE algorithm and procedure. Based on frequency measurements for damage detection, the inverse eigenproblem computation makes full use of the forward eigenproblem computation for frequency solutions. As a result, making the two forward and inverse complementary parts of the research series work together, the proposed FE procedure reduces the cost of computation and improves the accuracy of the solutions for determining the locations and sizes of cracks in beams.

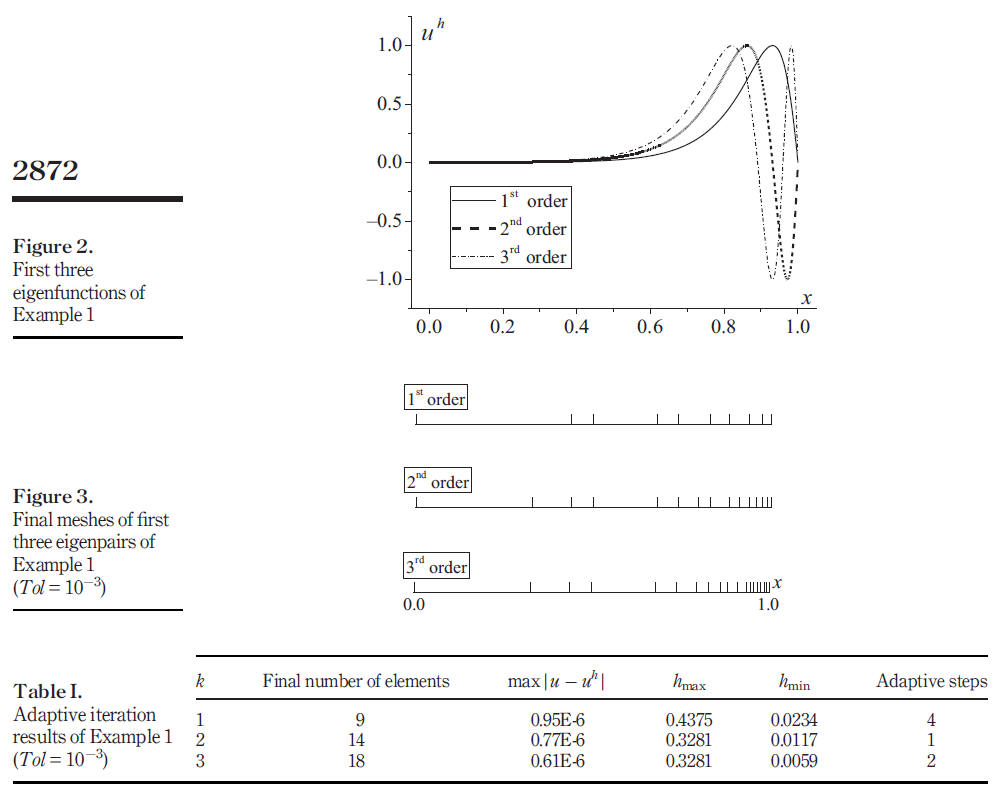
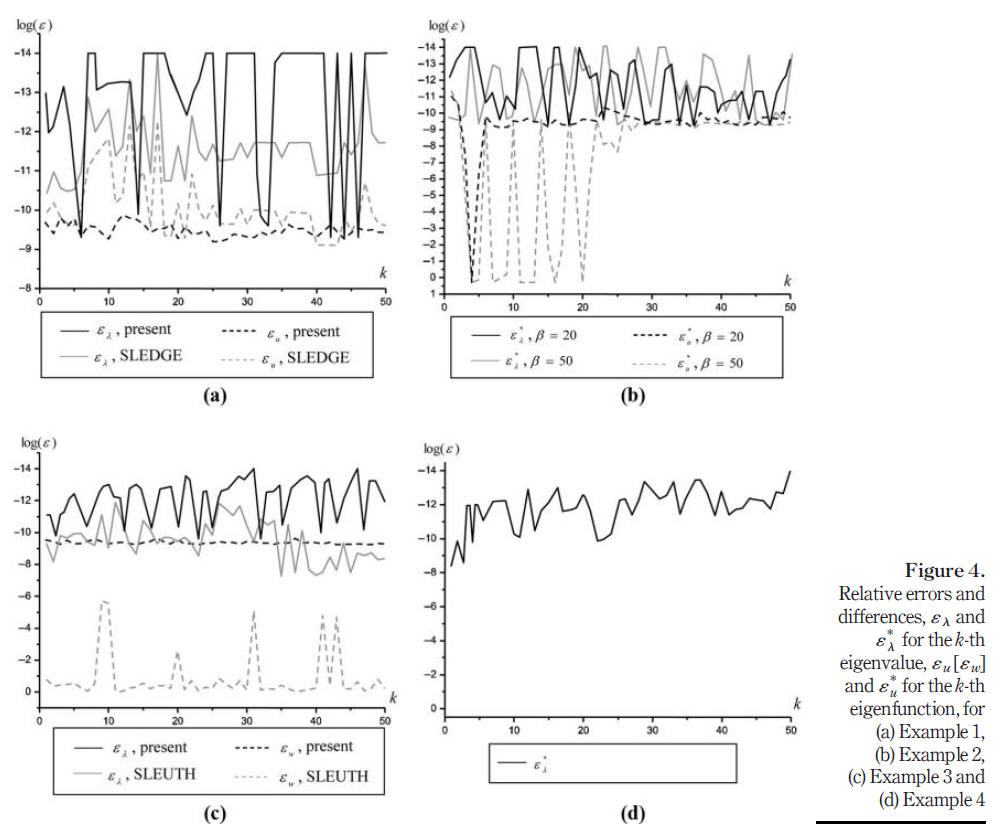
2. Si Yuan, Kangsheng Ye, Yongliang Wang, David Kennedy, Frederic W Williams. Adaptive finite element method for eigensolutions of regular second and fourth order Sturm-Liouville problems via the element energy projection technique. Engineering computation. 2017. 13(3): 78-92.

The purpose of this research is to present a numerically adaptive finite element (FE) method for accurate, efficient and reliable eigensolutions of regular second- and fourth-order Sturm–Liouville (SL) problems with variable coefficients. After the conventional FE solution for an eigenpair (i.e. eigenvalue and eigenfunction) of a particular order has been obtained on a given mesh, a novel strategy is introduced, in which the FE solution of the eigenproblem is equivalently viewed as the FE solution of an associated linear problem. This strategy allows the element energy projection (EEP) technique for linear problems to calculate the super-convergent FE solutions for eigenfunctions anywhere on any element. These EEP super-convergent solutions are used to estimate the FE solution errors and to guide mesh refinements, until the accuracy matches user-preset error tolerance on both eigenvalues and eigenfunctions. Numerical results for a number of representative and challenging SL problems are presented to demonstrate the effectiveness, efficiency, accuracy and reliability of the proposed method. Research limitations/implications – The method is limited to regular SL problems, but it can also solve some singular SL problems in an indirect way. Comprehensive utilization of the EEP technique yields a simple, efficient and reliable adaptive FE procedure that finds sufficiently fine meshes for preset error tolerances on eigenvalues and eigenfunctions to be achieved, even on problems which proved troublesome to competing methods. The method can readily be extended to vector SL problems.

3. To be supplemented... ...

Copyright ©2018 www.wangyongliang.net All Rights Reserved 京ICP: 16060549
Computational Rock Mechanics Research Group
State Key Laboratory of Coal Resources and Safe Mining, China University of Mining and Technology (BJ)
Email: wangyl@tsinghua.org.cn